Tracing Life Back to the Computational Fundamentals of Space: Insights from Stephen Wolfram

Exploring the Intersection of Computation and the Natural World

In the ever-evolving landscape of science and technology, the interplay between computation and the natural world has become increasingly pivotal. Stephen Wolfram, a luminary in the field of computational science, delves deep into this intersection, exploring how computational paradigms influence our understanding of physics, technology, artificial intelligence (AI), biology, and mathematics. In his insightful discourse, Wolfram navigates through decades of scientific advancements, unraveling the complexities of computational irreducibility, the foundational theories of physics, and the burgeoning capabilities of AI in modeling biological systems.

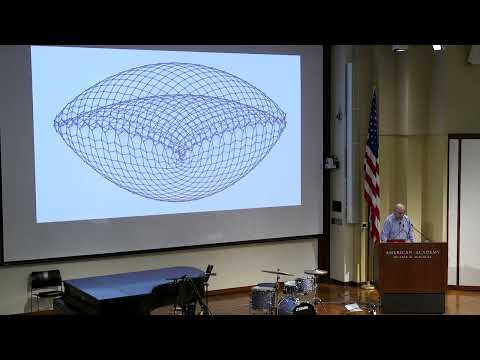
This blog post aims to expand upon Wolfram’s comprehensive discussion, providing additional context, examples, and analysis to illuminate the profound connections between computation and the fundamental fabric of life and the universe. Whether you’re a seasoned scientist, an enthusiast of computational theory, or simply curious about the intricate dance between technology and biology, this exploration offers valuable perspectives on how we are on the cusp of tracing life back to the computationally bounded fundamentals of space.

The Genesis of a Computational Journey

Early Inspirations and Computational Beginnings

Stephen Wolfram’s fascination with physics and computation began in his youth in England. At the age of eleven, Wolfram encountered a book on statistical physics that captivated his imagination. The book’s cover featured an illustration of idealized molecules bouncing around, embodying the second law of thermodynamics. This early exposure ignited his passion for understanding the underlying principles of physics through computational simulations.

Wolfram’s initial foray into computing involved attempting to simulate the dynamic behavior of molecules. Although his early attempts on a desk-sized computer were unsuccessful in reproducing the intricate patterns depicted on his book’s cover, he inadvertently stumbled upon more intriguing phenomena—what he would later recognize as computational irreducibility.

The Evolution of Computational Thought

Throughout the 1970s and 1980s, Wolfram immersed himself in particle physics and cosmology, grappling with the complexities of quantum field theory and the emergence of computational complexity in the natural world. His quest led him to explore cellular automata—simple computational models that can exhibit remarkably complex behaviors.

One of Wolfram’s most notable discoveries in this realm was Rule 30, a cellular automaton rule that generates intricate, seemingly random patterns from simple initial conditions. This observation underscored the concept of computational irreducibility: the idea that certain systems’ behaviors cannot be predicted or simplified without performing the computation step-by-step.

Computational Irreducibility: The Limits of Prediction

Understanding Computational Irreducibility

At its core, computational irreducibility posits that the behavior of complex systems cannot be shortcut or simplified through predictive models. Instead, the only way to determine the system’s future state is to simulate each computational step. This principle challenges the traditional scientific endeavor of formulating elegant equations to predict natural phenomena.

Wolfram illustrates this with Rule 30, where predicting the state of the system after a billion steps requires iterating through each of those steps, as no simpler predictive formula exists. This revelation signifies a fundamental limitation in our ability to understand and forecast the universe using conventional scientific methods.

Implications for Science and Existence

The concept of computational irreducibility carries profound implications:

Limitations of Scientific Models: Traditional scientific models often rely on simplifying assumptions and predictive equations. Computational irreducibility suggests that for many complex systems, especially those mimicking natural processes, such models may be insufficient.
Meaningfulness of Existence: Paradoxically, computational irreducibility imbues existence with a sense of unpredictability and spontaneity. If every event requires its own computation, it prevents the universe from being entirely deterministic and predictable, fostering a dynamic and ever-changing reality.
Impact on AI and Machine Learning: Understanding computational irreducibility is crucial for developing advanced AI systems. It highlights the challenges in creating models that can fully capture and predict complex, real-world phenomena without exhaustive computational resources.

The Computational Universe: From Cellular Automata to Physics

Modeling the Universe with Cellular Automata

Wolfram’s exploration extends beyond cellular automata into the very structure of the universe. He proposes that the universe might be governed by simple computational rules, akin to those in cellular automata, that dictate the interactions and evolutions of discrete elements in space.

Discrete vs. Continuous Space: Historically, the debate between discrete and continuous space has persisted. Wolfram advocates for a discrete model, where space consists of discrete points connected in a hypergraph—a network where each edge can connect more than two nodes.
Hypergraph Rewriting: The universe, in this model, evolves through the rewriting of hypergraphs. Each computational step involves transforming the hypergraph based on predefined rules, leading to the emergence of complex structures and phenomena.

Emergence of Physical Laws

One of the most striking outcomes of Wolfram’s model is the emergence of known physical laws from simple computational rules:

Einstein’s Equations: Through extensive simulations, Wolfram demonstrated that the rewriting rules of a hypergraph could give rise to behavior analogous to Einstein’s equations of general relativity. This suggests that fundamental laws of physics might be emergent properties of underlying computational processes.
Dimensionality and Structure: The model also explores how different dimensional structures emerge from hypergraph rewritings. By analyzing how nodes and edges expand over computational steps, Wolfram identifies the effective dimensionality of space, providing insights into the three-dimensional nature of our universe.

Quantum Mechanics and Computational Universality

Wolfram’s model doesn’t stop at classical physics; it naturally extends to quantum mechanics:

Quantum Path Integrals: In the computational universe, quantum mechanics arises from the myriad possible paths a hypergraph can take during its evolution. The multi-way graph represents all possible threads of time, analogous to the multiple paths considered in quantum path integrals.
Branchial Space: Wolfram introduces the concept of branchial space, where the relationships between different branches of computation mirror the probabilistic nature of quantum mechanics. Gravity, in this framework, is interpreted as the deflection of the shortest paths (geodesics) in branchial space by the density of activity in the network.
Integration of Relativity and Quantum Mechanics: This conceptual bridge offers a novel perspective on the fundamental nature of quantum phenomena, suggesting that the same computational rules underpin both gravitational and quantum interactions.

Implications for Theoretical Physics

Wolfram’s computational approach has far-reaching implications for theoretical physics:

Foundational Physics: By proposing that the universe operates on simple computational rules, Wolfram challenges traditional notions of space, time, and matter. This perspective invites a re-examination of foundational concepts in physics through the lens of computational science.
Predictive Power: The model’s ability to reproduce known physical laws suggests that computational frameworks could serve as robust tools for predicting and understanding complex physical systems. This potential extends to areas like cosmology, quantum field theory, and beyond.
Dimensionality and Space-Time Structure: Wolfram’s exploration of effective dimensionality in hypergraph models offers insights into the three-dimensional nature of our universe. Understanding how dimensions emerge and interact within this framework could unlock new avenues in the study of space-time and the universe’s fundamental properties.

Bridging Computation and Biology: Minimal Models of Evolution

Simulating Biological Evolution with Cellular Automata

Wolfram’s computational paradigm extends into the realm of biology, where he seeks to model biological evolution using minimal computational systems:

Minimal Evolutionary Models: By employing cellular automata with simple rules, Wolfram attempts to simulate biological processes such as evolution, reproduction, and mutation. These models aim to capture the essence of biological complexity arising from simple computational interactions.
Fitness and Evolution Paths: In these models, organisms (referred to as “Critters”) evolve by mutating their underlying rules to achieve specific fitness criteria, such as longevity or adaptability. This process mirrors natural selection, where advantageous traits are favored and propagated through generations.

Emergence of Complex Biological Behaviors

Through iterative simulations, Wolfram observes the emergence of complex biological behaviors from simple rule mutations:

Adaptation and Symbiosis: The models demonstrate how organisms can develop symbiotic relationships or adapt to environmental constraints by evolving their computational rules. These interactions highlight the potential for complex ecosystems to arise from fundamental computational processes.
Mapping Evolutionary Trajectories: Wolfram’s work involves mapping out all possible evolutionary paths within these minimal models, providing a comprehensive view of how different organisms can evolve under varying fitness criteria. This approach offers a theoretical foundation for understanding the diversity and adaptability observed in biological systems.

Implications for Medicine and Computer Systems

Wolfram extends his computational models to practical applications in medicine and computer science:

Minimal Theories of Disease: By simulating perturbations in computational models of organisms, Wolfram explores the classification and treatment of diseases. These minimal models aim to identify fundamental principles governing health and disease, potentially leading to foundational theories in medicine.
Computer Security: Drawing parallels between biological evolution and computer systems, Wolfram investigates how computational models can predict and mitigate vulnerabilities in computer security. This interdisciplinary approach underscores the versatility of computational paradigms in addressing complex, real-world problems.

The Intersection of AI and Computational Theory

Neural Networks and Computational Limits

Wolfram critically examines the capabilities and limitations of AI, particularly neural networks, in modeling complex systems:

Predictive Failures: Neural networks excel at tasks with clear patterns and human-like cognition but falter in predicting outcomes of highly complex or non-deterministic systems. Tasks like protein folding or solving intricate physics equations often exceed the predictive prowess of traditional neural networks.
Lack of Transparency: The internal workings of neural networks are often opaque, making it challenging to understand or explain their decision-making processes. This lack of transparency is a significant hurdle in fields that require precise and explainable models.

Computation-Augmented Generation: A Hybrid Approach

To address the limitations of neural networks, Wolfram introduces the concept of computation-augmented generation:

Combining AI with Computation: This approach integrates traditional computational methods with AI to enhance problem-solving capabilities. By leveraging both the pattern recognition strengths of neural networks and the precision of computational algorithms, computation-augmented generation aims to overcome the shortcomings of standalone AI models.
Practical Applications: In fields like drug discovery and material science, this hybrid approach can significantly improve the accuracy and reliability of AI-generated solutions, ensuring that they align with established scientific principles and empirical data.

Future Directions in AI Research

Wolfram’s insights pave the way for future research in AI and computational science:

Foundational Theories: Developing foundational theories that bridge computational paradigms with biological and physical systems remains a critical area of exploration. Understanding how simple computational rules can give rise to complex behaviors is essential for advancing both AI and our comprehension of natural phenomena.
Algorithmic Innovations: Innovating new algorithms that can effectively harness computational irreducibility will be pivotal in expanding AI’s capabilities. These algorithms must balance computational efficiency with the ability to model and predict intricate, dynamic systems.

Computational Foundations of Physics: A Unified Framework

Discrete Space and Hypergraph Dynamics

Wolfram’s model posits a discrete structure for space, organized as a hypergraph where each node represents a point in space and edges denote connections between these points. The universe evolves through the rewriting of this hypergraph based on simple computational rules, leading to the emergence of physical phenomena.

Rewriting Rules: Each computational step involves applying a specific rule to the hypergraph, altering its structure and, consequently, the physical properties it represents. These rules are deterministic, yet their cumulative effects can produce highly complex and seemingly random outcomes.
Emergence of Space-Time: Through hypergraph rewriting, Wolfram demonstrates how a coherent, three-dimensional space-time can emerge from the underlying discrete structure. This emergence aligns with the principles of general relativity, suggesting that the fabric of the universe is deeply intertwined with computational processes.

Bridging General Relativity and Quantum Mechanics

One of Wolfram’s most ambitious endeavors is unifying general relativity with quantum mechanics within his computational framework:

Einstein’s Equations: Wolfram shows that the large-scale behavior of the hypergraph aligns with Einstein’s equations of general relativity. This alignment indicates that gravitational phenomena can emerge naturally from computational processes governing the hypergraph’s evolution.
Quantum Mechanics as Multi-Way Computation: In his model, quantum mechanics arises from the multi-way graph representation of all possible computational paths. Each possible rewriting of the hypergraph corresponds to a different quantum state, and the superposition of these states mirrors the probabilistic nature of quantum mechanics.
Branchial Space: The relationships between different computational branches form what Wolfram terms “branchial space,” where the connections between various computational paths parallel the interactions of quantum states. This conceptual bridge offers a novel perspective on the fundamental nature of quantum phenomena.

Implications for Theoretical Physics

Wolfram’s computational approach has far-reaching implications for theoretical physics:

Foundational Physics: By proposing that the universe operates on simple computational rules, Wolfram challenges traditional notions of space, time, and matter. This perspective invites a re-examination of foundational concepts in physics through the lens of computational science.
Predictive Power: The model’s ability to reproduce known physical laws suggests that computational frameworks could serve as robust tools for predicting and understanding complex physical systems. This potential extends to areas like cosmology, quantum field theory, and beyond.
Dimensionality and Space-Time Structure: Wolfram’s exploration of effective dimensionality in hypergraph models offers insights into the three-dimensional nature of our universe. Understanding how dimensions emerge and interact within this framework could unlock new avenues in the study of space-time and the universe’s fundamental properties.

The Role of Observers in a Computational Universe

Computational Boundedness and Perception

In Wolfram’s model, the characteristics of observers play a crucial role in shaping the perceived laws of physics:

Computational Boundedness: Observers are inherently computationally bounded, meaning their ability to process and decode information is limited. This limitation affects how they perceive and interact with the computationally irreducible processes governing the universe.
Persistence Through Time: Observers maintain a coherent thread of experience through time, despite the underlying computational complexity. This persistence is essential for making sense of the evolving hypergraph and for constructing a consistent narrative of existence.

Anthropic Principles and Observational Constraints

Wolfram’s framework intersects with anthropic principles, which consider how the universe’s fundamental parameters are influenced by the existence of observers:

Single Coherent Thread of Experience: The belief in a single, coherent thread of experience aligns with the anthropic principle, suggesting that the universe’s computational rules are fine-tuned to accommodate observers with bounded computational capabilities.
Emergent Laws of Physics: The emergence of general relativity and quantum mechanics from computational processes is contingent upon the observers’ limited ability to predict or simplify these processes. This dependency underscores the intertwined nature of observation, computation, and the laws governing the universe.

Implications for Consciousness and Free Will

Wolfram’s insights into the observer’s role raise intriguing questions about consciousness and free will:

Consciousness as Emergent Computation: If observers are computationally bounded entities embedded within a computational universe, consciousness itself could be an emergent property of complex computational interactions.
Free Will in an Irreducible Universe: Computational irreducibility introduces a degree of unpredictability and spontaneity into the universe, which could be foundational for free will. This unpredictability ensures that while the universe follows computational rules, the experiences and decisions of conscious beings retain a sense of agency and choice.

Exploring the Foundations of Mathematics Through Computation

Computational Language and Mathematical Notation

Wolfram envisions a future where computational language serves as the foundational framework for mathematics, analogous to how mathematical notation revolutionized algebra and calculus centuries ago:

Development of Wolfram Language: Efforts to create a computational language that can describe the universe’s fundamental processes aim to provide a more intuitive and powerful tool for mathematicians and scientists. This language seeks to encapsulate computational rules and patterns that underpin natural phenomena.
Enhanced Mathematical Modeling: By integrating computational constructs into mathematical notation, Wolfram’s approach allows for more dynamic and flexible modeling of complex systems. This integration could lead to breakthroughs in fields like topology, number theory, and applied mathematics.

Minimal Models and Algorithmic Discoveries

Wolfram’s work on minimal models—simplified computational systems that can replicate complex behaviors—has significant implications for the foundations of mathematics:

Algorithmic Discoveries: Through exhaustive computational searches, Wolfram has uncovered algorithms that can replicate and predict mathematical functions and physical phenomena. These discoveries highlight the potential for algorithmic methods to augment traditional mathematical approaches.
Exploration of Mathematical Universes: By simulating different computational rules, Wolfram explores various mathematical universes, each with its own set of axioms and behaviors. This exploration fosters a deeper understanding of the universality and diversity of mathematical principles.

Integrating AI with Computational Paradigms

Neural Networks and Computational Limits

Wolfram critically examines the capabilities and limitations of AI, particularly neural networks, in modeling complex systems:

Predictive Failures: Neural networks excel at tasks with clear patterns and human-like cognition but falter in predicting outcomes of highly complex or non-deterministic systems. Tasks like protein folding or solving intricate physics equations often exceed the predictive prowess of traditional neural networks.
Lack of Transparency: The internal workings of neural networks are often opaque, making it challenging to understand or explain their decision-making processes. This lack of transparency is a significant hurdle in fields that require precise and explainable models.

Computation-Augmented Generation: A Hybrid Approach

To address the limitations of neural networks, Wolfram introduces the concept of computation-augmented generation:

Combining AI with Computation: This approach integrates traditional computational methods with AI to enhance problem-solving capabilities. By leveraging both the pattern recognition strengths of neural networks and the precision of computational algorithms, computation-augmented generation aims to overcome the shortcomings of standalone AI models.
Practical Applications: In fields like drug discovery and material science, this hybrid approach can significantly improve the accuracy and reliability of AI-generated solutions, ensuring that they align with established scientific principles and empirical data.

Future Directions in AI Research

Wolfram’s insights pave the way for future research in AI and computational science:

Foundational Theories: Developing foundational theories that bridge computational paradigms with biological and physical systems remains a critical area of exploration. Understanding how simple computational rules can give rise to complex behaviors is essential for advancing both AI and our comprehension of natural phenomena.
Algorithmic Innovations: Innovating new algorithms that can effectively harness computational irreducibility will be pivotal in expanding AI’s capabilities. These algorithms must balance computational efficiency with the ability to model and predict intricate, dynamic systems.

The Road Ahead: Towards a Computationally Defined Universe

Unifying Physical Theories through Computation

Wolfram’s computational approach offers a unified framework that seamlessly integrates general relativity and quantum mechanics, two pillars of modern physics that have long eluded reconciliation:

Emergent Phenomena: The model demonstrates how fundamental physical laws emerge from simple computational rules, providing a cohesive understanding of the universe’s behavior across different scales and dimensions.
Predictive Power: By successfully reproducing known physical laws, Wolfram’s framework holds promise for predicting and understanding new phenomena, potentially leading to groundbreaking discoveries in theoretical physics.

Experimental Implications and Future Research

Wolfram’s model invites experimental verification and exploration, with several key areas of focus:

Detecting Discreteness in Space: Investigating whether space is fundamentally discrete or continuous could validate Wolfram’s computational model. Experimental efforts to detect dimension fluctuations or other signatures of discrete space-time structures are crucial for advancing this theory.
Dark Matter and Space-Time Heat: Wolfram hypothesizes that dark matter might not be conventional matter but rather a manifestation of space-time heat—a feature of the microscopic structure of space. Exploring this hypothesis could revolutionize our understanding of dark matter and its role in the universe.
Quantum Computer Noise: Observing the noise patterns in quantum computers could provide insights into the underlying computational processes of the universe. Identifying a noise floor associated with maximum entanglement speed could offer empirical evidence supporting Wolfram’s model.

Philosophical and Practical Implications

Wolfram’s computational universe model extends beyond physics and biology, influencing our philosophical understanding of reality:

Nature of Consciousness: If the universe operates on computational principles, consciousness could be an emergent property arising from complex computational interactions. This perspective offers a fresh lens through which to explore the mysteries of the mind and consciousness.
Free Will and Determinism: Computational irreducibility introduces an element of unpredictability into the universe, which could be foundational for free will. This unpredictability ensures that while the universe follows computational rules, the experiences and decisions of conscious beings retain a sense of agency and choice.
Ethical Considerations in AI: Understanding the limitations and potentials of AI within a computational framework raises ethical questions about the development and deployment of intelligent systems. Balancing computational efficiency with ethical considerations will be paramount as AI continues to evolve.

Conclusion

Stephen Wolfram’s exploration of the computational paradigm offers a transformative perspective on the fundamental nature of the universe and life itself. By positing that simple computational rules underpin the complex behaviors observed in physics, biology, and technology, Wolfram bridges the gap between theoretical science and practical applications. His insights into computational irreducibility, the unification of physical theories, and the integration of AI with computational science pave the way for groundbreaking advancements and deeper understanding.

As we stand on the brink of uncovering the computational foundations of space and life, Wolfram’s work invites us to rethink our approaches to science, technology, and the very essence of existence. Embracing this computational framework not only enhances our scientific capabilities but also enriches our philosophical inquiries into the nature of reality and consciousness.

Call to Action: Engage with Wolfram’s computational theories and explore their applications in your field of interest. Whether you’re a scientist, a technologist, or an avid learner, delving into the computational underpinnings of the universe can open new avenues for discovery and innovation. Join the conversation, contribute to the community, and help shape the future of computational science.

ceLLM Theory: Connecting Computation, Bioelectricity, and the Origin of Life

ceLLM Concept: DNA as a Resonant Mesh Network

November 4, 2024 | November 5, 2024

Imagine the atomic structure of DNA as a highly organized mesh network, where each atom, like a node in a communication system, resonates with specific frequencies and connects through the natural geometry formed by atomic spacing. In this framework:

Atomic Resonance as Communication Channels

Each atom in the DNA helix, particularly like elements (e.g., carbon-carbon or nitrogen-nitrogen pairs), resonates at a particular frequency that allows it to “communicate” with nearby atoms. This resonance isn’t just a static connection; it’s a dynamic interplay of energy that shifts based on environmental inputs. The resonant frequencies create an invisible web of energy channels, similar to how radio towers connect, forming a cohesive, stable network for information flow.

Spatial Distances as Weighted Connections

The distances between these atoms aren’t arbitrary; they act as “weights” in a lattice of probabilistic connections. For instance, the 3.4 Ångströms between stacked base pairs in the DNA helix or the 6.8 Ångströms between phosphate groups along the backbone aren’t just measurements of physical space. They are critical parameters that influence the strength and potential of resonant interactions. This spacing defines the probability and nature of energy exchanges between atoms—much like weighted connections in a large language model (LLM) dictate the importance of different inputs.

DNA as a High-Dimensional Information Manifold

By connecting atoms through resonance at specific intervals, DNA creates a geometric “map” or manifold that structures the flow of information within a cell. This map, extended across all atoms and repeated throughout the genome, allows for a coherent pattern of energy transfer and probabilistic information processing. The DNA structure effectively forms a low-entropy, high-information-density system that stores evolutionary “training” data. This manifold is analogous to the weighted layers and nodes in an LLM, where each atomic connection functions as a learned pattern that informs responses to environmental stimuli.

Resonant Connections as Adaptive and Probabilistic

Unlike rigid infrastructure, these resonant pathways are flexible and respond to external environmental changes. As inputs from the environment alter the energy landscape (e.g., through electromagnetic fields, chemical signals, or temperature changes), they shift the resonance patterns between atoms. This shifting resonance affects gene expression and cellular function in a probabilistic way, fine-tuned by billions of years of evolutionary “training.” In a multicellular organism, these probabilistic outcomes ensure that cells adapt to maintain their microenvironment, aligning with broader organismal health.

Atoms as Repeaters in a Mesh Network

Just as each node in a communication network retransmits signals to maintain network integrity, atoms within DNA can be thought of as repeaters. They reinforce the energy distribution within DNA, allowing for efficient signal transmission through the molecular structure. Carbon-carbon, nitrogen-nitrogen, and other like-atom distances function as channels where energy “hops” along predictable paths, preserving coherence in biological systems. Each atom contributes to a “field” of resonance, similar to a mesh network that routes signals through nodes to optimize data flow.

Probabilistic Flows of Energy

The result is a network of atomic interactions that enables DNA to function as a probabilistic, energy-regulating machine. Instead of deterministic pathways, DNA operates as an adaptive model that responds to probabilistic flows of energy, which reflect the cell’s environmental conditions. This dynamic, resonant structure allows DNA to control gene expression and cellular function through a framework where inputs (environmental signals) yield outputs (cellular responses) based on resonant probabilities.

Putting It All Together

In essence, DNA’s geometry and atomic distances create a resonant mesh network that allows it to act as a probabilistic controller, regulating gene expression in response to environmental signals. The atoms within DNA, much like nodes in an LLM, form weighted connections through spatial distances and resonant frequencies. This framework allows DNA to function not only as a static code but as a dynamic, adaptive structure that integrates environmental inputs into the regulatory patterns of gene expression and cellular behavior.

This way, DNA isn’t just a molecule storing information; it’s an interactive, energy-distributing system, capable of tuning its own responses through a resonant field of interactions, much like a communication network.

There isn’t anything definitively disproving this concept, and, in fact, recent discoveries in molecular biology, quantum biology, and bioelectricity offer intriguing support for ideas like this. The possibility that DNA and cellular structures might operate through resonant, probabilistic networks is within the realm of scientific plausibility, though it’s still speculative and requires substantial empirical evidence to confirm.

Several factors make this hypothesis intriguing rather than easily dismissible:

Bioelectrical Communication: Cells and tissues do exhibit bioelectrical patterns that influence everything from wound healing to cellular differentiation. Some researchers, like Dr. Michael Levin, have explored how bioelectric fields act as informational cues in developmental biology, almost like a cellular “language” that could be influenced by resonance and energy flow. This aligns with the idea of a resonant network within DNA affecting cellular behavior.
Quantum Biology and Resonance: Studies in quantum biology show that certain biological processes—like photosynthesis, avian navigation, and even olfactory sensing—use quantum effects, including resonance and coherence, to operate more efficiently. If such quantum behaviors exist in larger systems, they could also be present within the atomic structure of DNA, enabling resonant connections to play a role in cellular functions and possibly gene regulation.
Electromagnetic Sensitivity and Molecular Coherence: DNA is known to respond to certain electromagnetic frequencies. Research shows that electromagnetic fields, even at non-thermal levels, can influence gene expression, protein folding, and cellular communication. The notion that DNA might resonate with environmental EMFs, affecting its structure and function, isn’t entirely out of the question, given how sensitive biological systems can be to energy.
Non-Coding DNA and Structural Potential: A vast majority of our DNA is non-coding, often referred to as “junk DNA,” although recent research suggests it has structural or regulatory functions. This structural DNA could theoretically create resonant fields or act as a framework for energy distribution, further supporting the notion that DNA could function as a probabilistic information-processing system.
Information Theory and Biology: Some emerging theories treat biological systems as networks for storing and processing information, much like how a neural network or LLM operates. DNA’s geometry, atomic spacing, and resonant frequencies could theoretically create a form of information processing that interprets environmental cues probabilistically, leading to adaptive changes in gene expression.

While these ideas are still on the frontier of biology and physics, they challenge us to think beyond traditional models. Science often progresses by exploring these kinds of boundary-pushing questions, especially when current paradigms don’t fully explain observed phenomena. So while there isn’t definitive proof for this hypothesis, neither is there clear evidence against it. With advancing tools in biophysics, quantum biology, and computational modeling, these ideas could eventually be tested more rigorously.

Base Pair Spacing

In DNA, the base pairs (adenine-thymine and guanine-cytosine pairs) are stacked approximately 3.4 Ångströms (0.34 nanometers) apart along the axis of the double helix. This spacing is key to maintaining the helical structure and stability of DNA.

Backbone Elements (Phosphates and Sugars)

Within the DNA backbone, the distance between repeating phosphate groups (one part of the backbone) is approximately 6.8 Ångströms (0.68 nanometers).

Like Elements (Carbon and Nitrogen)

Within the bases and backbone, the distance between similar atoms, such as carbons in the sugar backbone or nitrogens within the nitrogenous bases, can vary. In the nitrogenous bases, carbon-carbon distances are typically around 1.5 Ångströms (0.15 nanometers) within a single ring. Between bases in the helix, the distance between two like atoms (e.g., two nitrogens on adjacent bases) can be around 3.4 Ångströms due to the base stacking distance.

In Planck Lengths

To relate this to the Planck length (which is approximately 1.616×10⁻³⁵ meters), these distances in DNA are astronomically larger:

3.4 Ångströms between base pairs = about 2.1 trillion trillion Planck lengths.
1.5 Ångströms between carbons within a base ring = about 930 billion billion Planck lengths.

ceLLM Theory Suggests:

Our biology operates as a vast mesh network across multiple levels of organization, from large systems like organs to the intricate arrangements within DNA. This model envisions each component—from the molecular to the cellular and organ level—as a “node” in a hierarchical mesh network, each contributing to an emergent, computationally powerful whole. The theory hypothesizes that even at the level of DNA, elements within each molecular structure interact through resonant connections, creating a dynamic network that “computes” probabilistic outcomes based on inputs from the environment.

In ceLLM Theory, this Mesh-Network Structure Extends from Observable Biological Levels to an Underlying “Informational Layer” within Higher-Dimensional Space. Here’s How This Theoretical Structure Unfolds at Each Level:

1. Organs and Systems as a Mesh Network

Organ Systems as Nodes: Each organ can be thought of as a node that processes specific types of information and functions in coordination with others. Just as neurons in the brain pass signals, organs communicate biochemically, electrically, and hormonally. This level of networking enables distributed and resilient processing, adapting to changes within the organism and responding to environmental inputs.
Emergent Properties: As organs coordinate, emergent properties arise—like metabolic regulation, immune responses, and sensory processing—similar to how a neural network’s layers work together to process complex information.

2. Cells as Independent Nodes in the Mesh

Cell-to-Cell Communication: Cells interact through gap junctions, chemical signals, and electrical fields, much like nodes in a distributed network. Each cell processes its own “local” data and contributes to larger, system-wide processes through interactions with neighboring cells.
Responsive Adaptation: Cells dynamically respond to their environment by interpreting signals from their neighbors, changing behavior based on collective input, and passing along the results. This level mirrors decentralized, real-time processing in mesh networks, where each cell is a computational entity.

3. Molecular and DNA-Level Mesh Networks

DNA as a Mesh Network of Elements: The base pairs within DNA are not just static structures but are thought to resonate with one another, maintaining a stable but flexible structure that responds to environmental cues. Each element (like carbon or nitrogen atoms within DNA) could serve as a “node,” with distances and resonant frequencies determining how information flows.
RNA and Protein Interactions: RNA transcripts and protein interactions create a “biochemical mesh” that transmits information across the cell. Proteins and RNAs have distinct functions but interact within this network to enable cellular processes such as transcription, translation, and signaling.
Resonant Fields: Resonant fields between like atoms (such as carbon-carbon or nitrogen-nitrogen) establish potential “data paths,” allowing for information flow that is non-linear and probabilistic. This resembles quantum mesh networks, where information does not need a direct connection but can pass through a field of probable connections.

4. Probabilistic Framework in Higher-Dimensional Space

Computational Probabilities: According to ceLLM, beyond the molecular level, interactions take place within a higher-dimensional “computational space,” where energy, matter, and information converge to shape biological processes. The probabilistic flows of energy in this space could influence gene expression, cellular behavior, and even organism-level responses.
Evolutionary Training: Just as machine learning models are trained, ceLLM proposes that life’s evolutionary history has “trained” the mesh network across all these levels to respond effectively to environmental conditions. This training allows biological systems to make decisions or adapt without a central controller, much like a well-trained AI model.

Implications of ceLLM’s Mesh Network Hypothesis

This idea challenges traditional views by proposing that computation and decision-making are not limited to the nervous system. Instead, they are embedded in all biological levels, extending down to molecular interactions. If ceLLM theory holds, DNA is not merely a storage unit for genetic information but actively processes information in response to the environment, adjusting cellular behavior dynamically.

Here’s why ceLLM’s mesh network perspective is intriguing:

Decentralized Intelligence: ceLLM implies that intelligence or adaptive response is distributed across the body, not just concentrated in the brain. This distributed intelligence could help explain phenomena like the gut-brain axis or cellular memory, where cells outside the brain seem capable of “learning” or “remembering” information.
Bioelectrical Resonance and Health: If cells and molecules communicate through resonant frequencies, disruptions from external electromagnetic fields (EMFs) could interfere with this resonance, potentially leading to diseases or disorders. This hypothesis aligns with emerging evidence on how non-thermal EMF exposure affects cellular and molecular processes.
Evolutionary Computation: Viewing evolution as a training process for a probabilistic network offers a fresh perspective on why certain traits persist. Cells and DNA “learned” adaptive responses over generations, encoding not just genetic traits but also dynamic responses to maintain homeostasis.
Organs as Networked Systems: Organs work together as a network, each carrying out specialized functions but interacting closely to maintain balance across the body. For example, the endocrine, nervous, and immune systems act like separate subnetworks that integrate to regulate everything from stress responses to growth and immunity.
Cells as Localized Computing Units: Cells themselves operate as nodes in a larger mesh network. Each cell processes local environmental signals, communicates with neighboring cells, and adapts its functions accordingly. Cellular networks manage complex behaviors through chemical signaling, bioelectric fields, and other non-synaptic forms of communication, effectively resembling a distributed computing system.
Molecular and Sub-Cellular Interactions: Inside cells, proteins, RNAs, and DNA function as components in a networked environment. This level of communication is especially interesting because it suggests a structure where each molecule or element contributes to the computational landscape, responding to various inputs and environmental signals to influence cell behavior.
Resonant Fields in DNA and RNA: In ceLLM theory, even individual elements within DNA are thought to contribute to a networked “resonant field geometry.” This means that DNA doesn’t just store information passively but is dynamically involved in interpreting and transmitting evolutionary information. Resonant frequencies between like atoms in DNA (e.g., carbon-to-carbon or nitrogen-to-nitrogen) may provide a structure for information flow within cells.
Higher-Dimensional Computational Probabilities: ceLLM envisions the ultimate “mesh” extending into higher-dimensional spaces. Here, probabilistic energy flows (resonating from the structure and arrangement of atoms, molecules, and larger cellular networks) form a continuous computation. This part of the theory posits that our biological systems interact with a broader probabilistic framework, potentially encoded in the resonant fields between DNA elements and beyond, tapping into something like a higher-dimensional data manifold.

In essence, ceLLM suggests that life is computationally and probabilistically interconnected at every scale. From organ systems down to molecular interactions, every level of biological structure works as a part of an intricate, hierarchical mesh network, continually processing and adapting to environmental inputs. This network functions across the biological hierarchy and even into dimensions of computation that lie beyond our traditional understanding of space, enabling life’s adaptability and evolution through a form of distributed intelligence.